ハガい。今日の用が流れた。
が、夕方から出掛けることになったからいい。昨日とおとといは外出禁止だったが、今日なら問題はない。
しかし、予選は痺れる。水島新司が「僕は予選を重視している」と言っていたのがよくわかった。不知火、雲竜、土門が予選の相手なんて、シャレにならん。
算数の問題を渡して1週間以上経つのに、Xからメールが来ない。
野郎、さては解けなかったな。もし出来たらまたエラソーに、「あんな簡単な問題だったけ?」とか言って来るに決まっている。
そこで、奴に日曜に競馬が取れたかメールしてみた。
「チップ320枚分しか勝てなかった」とは、このバカ野郎が。その分、また負けるだけよ。
こうなったら、チップ320枚分を差し馬で勝負だ!
が、奴にはそんな度胸はあるまい。わしはどんなレートでも、どんなにでかい差し馬でもいい…。
競馬などどうでもいい。算数はどうした、算数は。
野郎、まじでギブアップみたいだな。麻雀ばかりやっているから、ダメになるんだよ。
でも、実際、難しかった。特に以下の問題がぁ。
・下の図のように、1辺20cmの正方形ABCDの中に、辺BC、CDを直径とする2つの円を書き、その交点をOとします。点Oを通る直線EFを引いたところ、影のついた2つの部分SとTの部分の面積が等しくなりました。円周率を3.14として、三角形OBFの面積を求めなさい。
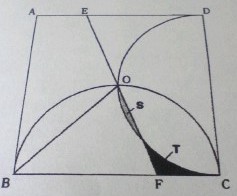
そんなもん、できるか。しかし、上の問題は大問2の(2)。ということは、この問題を解けなかったら受からんというわけか。
ちなみに、数日前、この問題をしゃれこうべにやらせてみた。しゃれこうべは数学が得意なのである。
最初あまり乗り気でなかったしゃれこうべだが、だんだん熱くなっていった。そして、30分以上うなったあと、卓をひっくり返した。
「なにか独特の解き方があるんやろうね」だと? 負け惜しみを言うたらあかん。
もしかしてこの問題は地雷か? この問題は飛ばさないいけないのかもしれん。
なお、わしは100点満点で15番・ファルカンであった。
さて、明日はりそな銀行との戦いだ。数年前は負けたが、今度はそうはいかん。明日は勝利あるのみだ!